앞서 공부한 통계기법에 이어서
이제 확률에 대해서 공부하고자 한다
역시나 참고한 강의는 메타코드m강의
https://mcode.co.kr/mypage/lecture_view?wm_id=993&lecture_id=8&lecture_num=4&lecture_sub=43
메타코드M
빅데이터 , AI 강의 플랫폼 & IT 현직자 모임 플랫폼ㅣ메타코드 커뮤니티 일원이 되시기 바랍니다.
mcode.co.kr
확률과 확률변수
1. 표본공간
: 실험에 의해 나타날 수 있는 가능한 모든 결과의 집합
2. 사건
: 표본공간의 부분집합
3. 확률
: 표본 공간의 부분집합인 사건A의 확률은 표본 공간의 원소 개수에 대한 사건A의 원소 개수 비율
P(A) = N(A)
4. 확률 진리
1) 0<= P(A) <= 1
2) P(S) =1
3) 서로 배반사건이면 P(AUB) = P(A) + P(B)
5. 확률 계산
1) 덧셈법칙
2) 곱셉법칙
-A와 B가 독립이면 P(AUB) = P(A) * P(B)
6. 조건부 확률
: 조건이 주워질때 사건A가 일어날 확률
-A가 일어났을 때 B가 일어날 확률 P(A|B) = A와 B의 교집합 / P(A)
-B가 일어났을 때 A가 일어날 확률 P(B|A) = A와 B의 교집합 / P(B)
7. 독립사건과 종속사건
1) 독립사건 : 각 사건이 서로 영향을 주지 않음
P(A|B) = P(A)
P(B|A) = P(B)
2) 종속사건 : 각 사건이 서로 영향을 줌
8. 베이즈정리
: 사전확률을 사후확률로 전환 가능

=> 사건 B가 발생함으로써 사건 A의 확률이 어떻게 변하는지를 표현한 것임
9. 확률변수
: 표본공간이 정의역, 실수값이 치역 함수

10. 확률 분포
: 확률 변수의 값과 확률을 대응시켜서 표나 그래프로 표현한 것
-확률의 합은 1임
11. 이산화확률변수/연속확률변수
: 확률변수의 확률함수를 알고 있다면 사건이 일어날 확률을 계산할 수 있음
1) 이산확률변수 : 이산점에서 0이 아닌 확률값을 가지는 확률변수 - 막대그래프
2) 연속확률변수 : 특정 실수 구간에서 0이 아닌 확률값을 가지는 확률 변수(특정점 아님)
12. 확률변수의 기댓값(평균)
1) 이산확률변수

=> 각각의 X의 가능한 값을 확률변수와 전부 곱하고 더하기 = 1
2) 연속확률변수
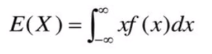
3) 기댓값(평균)의 성질
E(a) = a
E(aX+b) = aE(X) + b
E(aX+b) = aE(X) + bE(Y)
13. 확률변수의 분산과 표준편차
1) 분산 : 편차(개별값 - 평균값)의 제곱의 기댓값(평균)
*모분산, 표본분산 일 경우 N 또는 N-1 만큼 나눠주기
2)표준편차 : 분산에 제곱근을 취한값 (원래 값)
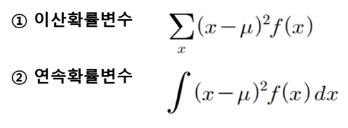
3) 분산의 성질
V(a) = 0
V(aX+b) = a^2V(X)
V(aX+b) = aV(X) + b^2V(Y)
4) 표준편차의 성질
6(a) = 0
6(aX+b) = a6(X)



